HOG Feature Descriptor-An Intuitive Overview

YUP !! In this post we will be looking at one of the most popular feature descriptor called Histogram of Oriented Gradients (HOG), proposed by Navneet Dalal and Bill Triggs in their paper Histograms of Oriented Gradients for Human Detection. Do Give it a Read 🖖🏽, but first get started..

Introduction

HOG is a feature descriptor that counts the number of times the gradient orientation falls into each of the histogram bins in a local region of the image. Gradient, orientation, bin are the terms that we will be looking at in this post, while understanding the algo of this descriptor.

In simple words Feature descriptor is something that provides a compact representation of an image. It is used to describe the image in a way that it can be used for classification.

{} Flow of the HOG Descriptor

1.Image Preprocessing

Size: Takes image of any size and resizes to [128x64] pixels.

Why ? Original HOG paper was suggested for pedestrian detection, ratio of 2:1 (height:width) of a human makes sense. Though we can use any size of the ratio 2:1.

Colour: For simplicity we will use grayscale image, but we can use colour images. In fact colour images performs better.

2.Gradient Calculation

Gradient is nothing but small change in the intensity of each pixel. Here we will be calculating the gradient in both x and y direction. Easily achievable by filtering the image with
\(\begin{bmatrix}-1 & 0 & 1 \end{bmatrix} \begin{bmatrix}-1 \\ 0 \\ 1 \end{bmatrix}\) for x & y axis respectively .
Same thing mathematically written as,
\(G_{x} \big(r, c\big) = I \big(r, c+1\big) - I \big(r, c-1\big)\)
\(G_{y} \big(r, c\big) = I \big(r+1, c\big) - I \big(r-1, c\big)\)

where $G_{x}$ is the gradient in x direction and $G_{y}$ is the gradient in y direction & $I$ is the intensity of the pixel at location $(r,c)$ in the matrix.

Basic idea is that, gradient of particular pixel is the difference between intensity of following pixel and previous pixel. Lets look at an example, EX: 1

\(mat = \begin{bmatrix}1 & 2 & 1 \\ 0& 0 & 1 \\ 3 & 2 & 1 \end{bmatrix}\)
\(G_{x} \big(2, 1\big) = I \big(2, 1+1\big) - I \big(2, 1-1\big)= I \big(2, 2\big) - I \big(2, 0\big) = 1 - 3 = -2\)
\(G_{y} \big(1, 2\big) = I \big(1+1, 2\big) - I \big(1-1, 2\big) = I \big(2, 2\big) - I \big(0, 2\big) = 1 - \big(-1\big) = 2\) Finally,
\(G_{x} = \begin{bmatrix}0 & 1 & -0.5 \\ 1 & 0 & -0.5 \\ -1.5 & 0 & -0.5 \end{bmatrix} G_{y} = \begin{bmatrix}0 & 1 & -0.5 \\ 1 & 0 & -0.5 \\ -1.5 & 0 & -0.5 \end{bmatrix}\)

Using the \(G_{x}, G_{y}\) values, we intend to calculate gradient magnitude and gradient orientation.

Gradient Magnitude is the magnitude of the vector formed by \(G_{x}\) and \(G_{y}\). In simple words it refers to the strength of an image’s intensity change.
Gradient magnitude \(\big(\mu \big)\) = \(\sqrt{G_{x}^{2} + G_{y}^{2} }\)

Whereas, Gradient Orientation is the angle of the vector formed by gx and gy. It refers direction of an image’s maximum change in intensity.
Gradient Orientation \(\big(\theta \big)\) = \(\tan^{-1} \big( \frac{G_{y}}{G_{x}} \big)\)

The gradient orientation is invariant to the rotation of the image. This means that the same object in an image will have the same gradient orientation regardless of the object’s orientation.

Gradient Magnitude & Gradient Orientation of matrix mat of EX 1:
\(magnitude, \mu = \begin{bmatrix}1 & 1 & 1.118 \\ 1 & 0.5 & 0.5 \\ 1.581 & 0 & 1.118 \end{bmatrix} orientation, \theta = \begin{bmatrix}0 & 1.57 & 0.46 \\ 1.57 & 0 & -1.57 \\ 1.892 & 0 & -0.464 \end{bmatrix}\)

For colour images, we calculate separate gradients for each colour channel, and take the one with the largest norm as the pixel’s gradient vector .

3.Histogram Calculation

The idea is to have some nonlinearity. Some kind of arrangement or engagement of magnitude & orientation matrix such that it can be used to depict the image.

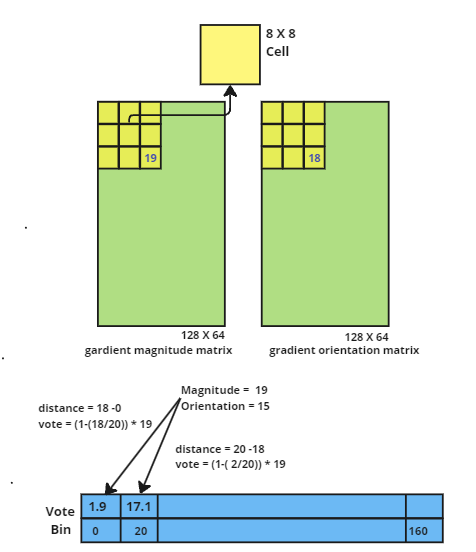
According to proposed paper, we make histogram with 9 bins for each [8x8] cell. The bin is selected based on the orientation value and the vote(the value that goes into the bin) is selected based on the magnitude.

Why 9 bins ? Bin is the range of values which is divided into a series of intervals. The authors of the paper has taken angles between [0, 180]. Basically meaning gradient angle and its negative is represented by the same number.

Empirically it has been shown that signed gradients work better than unsigned gradients for pedestrian detection. However including sign information does help substantially some other object recognition tasks, e.g. cars, motorbikes. Why histogram is generated for cell of pixels not for individual pixel? it provides a compact representation, lesser computational cost & makes this representation more robust to noise. Why 8x8 cell ? its basically a design choice, as we know HOG was for pedestrian detection , so 8X8 cell size is enough to capture the features of a human body like head or face.

There are many ways to implement the histogram, but the most common one is the linear interpolation. In this, the vote is distributed to the neighboring bins based on the distance from the centre of the bin. Mathematically \(vote = magnitude * \big(1 - \frac{distance}{bin size} \big)\)

Why linear interpolation ? It is used to distribute the vote of a pixel to the neighboring bins, a Way to have some spatial information.

The contributions of all the pixels in the 8×8 cells are added up to create the 9-bin histogram.

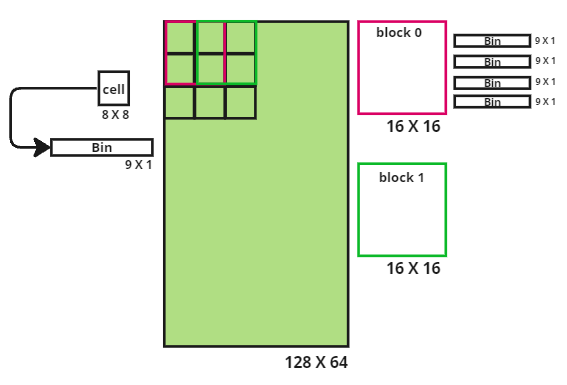
We have [128x64] pixel image. we divide it into sub [8x8] cells, so we have in total [16x8] (128/8=16, 64/8=8) cells. For each cell we calculate the histogram of 9 bins. So, we have 16* 8* 9 = 1152 bins.

4.Block Normalization

Depending upon the source of light, different parts of the images are illuminated differently. So, we need to normalize the histogram. So that our descriptor is independent of lighting variations.

How light affects the image ? Light affects the image by changing the intensity of the pixels. if image is illuminated by light from the left side, then the pixels on the left side will have higher intensity than the pixels on the right side. Gradient magnitude is directly proportional to the intensity of the pixel. So, the gradient magnitude will be higher on the left side than the right side. Note : Gradient orientation is independent of the intensity of the pixel.

We divide the image into blocks of size [16x16] pixels with stride 8 pixel. Remember we have [128x64] pixel image divided into [16x8] number of cells of size [8x8]. We want to have [16x16] block, so selecting 4 cells of [8x8] we get 1 block, and with stride=1 we have [7x15] blocks. For each cell we had 9 bins. Each block has 4 cells. That means each block has 4*9 = 36 bins, lets call this vector of 36 bins as a feature vector.
Written as \(f_{bi} = \begin{bmatrix} b0 & b1 & .... & b35 \end{bmatrix}\)

why 16x16 block ? The authors of the paper has taken block size of 16x16 pixels with a stride of 8 pixels. This means that the blocks overlap by 50%. This is done to capture the spatial information of the image.

To achieve normalization, we divide the feature vector of each block by the sum of the squares of the feature vectors of all the blocks in the block normalization window.
Mathematically, \(f_{bi} \leftarrow \frac{f_{bi}}{ \sqrt[]{ \parallel f_{bi} \parallel^{2} + \varepsilon } }\) this nothing but L2-normalization, where \(\varepsilon\) is a small constant to avoid division by zero.

4.Features Of Image

Since there are [7x15] blocks, we will have 7* 15 feature vectors, in total 7* 15* 36 = 3780 features. Similarly we will pass images to this descriptor and get the feature vector of the each image. This feature vector can be used for classification.

References

[1] What Is Gradient Orientation and Gradient Magnitude?
[2] HOG (Histogram of Oriented Gradients): An Overview
[3] Feature Engineering for Images: A Valuable Introduction to the HOG Feature Descriptor
[4] Implementation of HOG for Human Detection
[5] Histogram of Oriented Gradients explained using OpenCV
[6] First Pic credit